Understanding and visualizing a distance matrix

My PhD student has just received the data from a set of RNA samples analysed using a gene array. We discussed what should be done first to analyse these experiments. A good first step is to look at the distance between the samples and do unsupervised hierarchical clustering of all the samples to see how the biological replicates gather together. This represents an unbiased way to do some quality control for your experiments. Rather than just trying to identify different genes, we use all the data to determine if replicates gather together, if we have any outliers and to find patterns in the data. 

The first step is the generation of a distance matrix. A distance matrix tells us the difference between lists of numbers. If we put together a group of samples, then the distance matrix compares all of the samples. We discussed the purpose of the data matrix and visualising the matrix. I've written the following R script that tries to explain the concept. Mel helped me develop the script to visualise it using a script from this very informative Stack Overload post. 

Here is the a visualisation of a distance matrix using published data (Webber et al, 2014): 

Visualisation of distance matrix using data from Webber et al, 2014 

This distance matrix is used to do the hierarchical clustering that is plotted out here and shown here: 

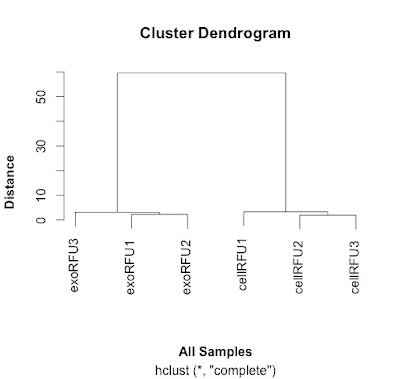Clustering samples using data from Webber et al, 2014.

# Trying to explain the concept of distance
# simple example 1: one digit different by 2 between two samples
samp1 <- c(0, 1, 2, 3, 4, 5, 6, 7, 8)
samp2 <- c(0, 1, 2, 3, 4, 5, 6, 7, 10)
dist(rbind(samp1, samp2))
# the dist() function compares each of the numbers in order along the two rows of the matrix. 
# answer is in this case is 2, as one number in the list is different by 2 to another. 

# simple example 2: one digit different by 72 between two samples
samp1 <- c(0, 1, 2, 3, 4, 5, 6, 7, 8)
samp2 <- c(0, 1, 2, 3, 4, 5, 6, 7, 80)
dist(rbind(samp1, samp2))
# answer is 72

# a little more complicated: two digits different
samp1 <- c(0, 1, 2, 3, 4, 5, 6, 7, 8)
samp2 <- c(0, 10, 2, 3, 4, 5, 6, 7, 80)
dist(rbind(samp1, samp2))
# now the answer is 72.56
# why? 
# well because of the equation used by the default method. 
# the default for the dist() function is euclidean 
# the equation for this is dist = sqrt(sum(x_i - y_i)^2)
# in this case, this calculates as sqrt(9^2 + 72^2)
# why the sqrt and the sum - in part so that the negatives and the positive differences don't cancel each other out.

# you can use other methods of calculating distance
help(dist)

# another is the "maximum" which just gives us the largest difference between the two arrays
# "Maximum distance between two components of x and y"
samp1 <- c(0, 1, 2, 3, 4, 5, 6, 7, 8)
samp2 <- c(0, 10, 2, 30, 4, 5, 6, 7, 80)
dist(rbind(samp1, samp2), method="maximum")
# in this case 72

# a third is the "manhattan" which sum of the absolute distances between the vectors
# "Absolute distance between the two vectors"
samp1 <- c(0, 1, 2, 3, 4, 5, 6, 7, 8)
samp2 <- c(0, 10, 2, 3, 4, 5, 6, 7, 80)
dist(rbind(samp1, samp2), method="manhattan")
# the answer now is 81

# now just envisage a more complicated situation when there are lots more numbers
# more than two samples and numbers that are higher and lower. 

# let's take a couple of examples from some data we analysed previously:

# http://www.mcponline.org/content/13/4/1050.full
# supplementary data is here: http://www.mcponline.org/content/suppl/2014/02/06/M113.032136.DC1/mcp.M113.032136-5.xlsx
# install if necessary:
# install.packages("readxl")
library(readxl)

# this is the link to the data
link <- "http://www.mcponline.org/content/suppl/2014/02/06/M113.032136.DC1/mcp.M113.032136-6.xlsx"

# the download.file() function downloads and saves the file with the name given
download.file(url=link,destfile="file.xlsx", mode="wb")

# then we can open the file and extract the data using the read_excel() function. 
data<- read_excel("file.xlsx")

View(data)

# the data has 762 observations. 

# we can only calculate distances in a matrix where all the values are the same mode - e.g numbers
# convert data frame (data) into a matrix 
# only want a subset of the data - the data from the samples. 
data.m <- as.matrix(data[2:7])
# transpose the data because a distance matrix works in rows
data.m.t <- t(data.m)

# calculate the distances and put the calculations into an object called distances
distances <- dist(data.m.t)

# convert this distances object into a matrix. 
distances.m <- data.matrix(distances)

# you can look at this object.
View(distances.m)

# we can extract the size of the object and the titles
dim <- ncol(distances.m)
names <- row.names(distances.m)

# now to create the visualisation of the difference matrix. 
# first the coloured boxes
image(1:dim, 1:dim, distances.m, axes = FALSE, xlab = "", ylab = "")

# now label the axis
axis(3, 1:dim, names, cex.axis = 0.8, las=3)
axis(2, dim:1, names, cex.axis = 0.8, las=1)

# add the values of the differences
text(expand.grid(1:6, 6:1), sprintf("%0.1f", distances.m), cex=1)

# this example lacks subltety
# the exo samples are very close together and the cell samples are quite far apart.
# it explains why the cluster analysis is so dramatic. 

# export this image as a tiff file with width of 1000 seems to work well. 
# some of the other formats don't work as well. 

# to make the cluster dendrogram object using the hclust() function
hc <- hclust(distances) 
# plot the cluster diagram
# some interesting groups in the data
plot(hc, 
     xlab =expression(bold("All Samples")), 
     ylab = expression(bold("Distance")))
# replicates cluster together well. 



The visualisation was inspired by this:

• http://stackoverflow.com/questions/3081066/what-techniques-exists-in-r-to-visualize-a-distance-matrix

If you have feedback on this script, please leave a comment.